Observée par un astronome au 19ème siècle, puis par Frank Benford en 1938, la loi de Benford énonce que dans une liste de données statistiques, le premier chiffre non nul le plus fréquent est le 1 (30.1%), puis le 2 (17.6%), lui même plus fréquent que le 3 (12.5%) jusqu'au chiffre 9 (4.6%). Or, cette loi est particulièrement intéressante dès lors qu'il s'agit de détecter la fraude notamment fiscale, comptable ou électorale au sein d'un jeu important de données.

En effet, la fraude a tendance à générer des anomalies qu'il est possible de révéler en confrontant les données douteuses aux données dictées par la loi de probabilité de Benford. Mais cette loi est psychologiquement difficile à appréhender tant elle apparaît comme un paradoxe : il y a en effet une tendance humaine à considérer que l'aléatoire implique forcément l'uniformité (ce qui revient à penser qu'on dénombrerait autant de premiers chiffres 1 que de 2, 3 etc... jusqu'à 9).

En réalité, voici les fréquences relatives d'apparition des premiers chiffres d'une série de nombres selon la loi de Benford :

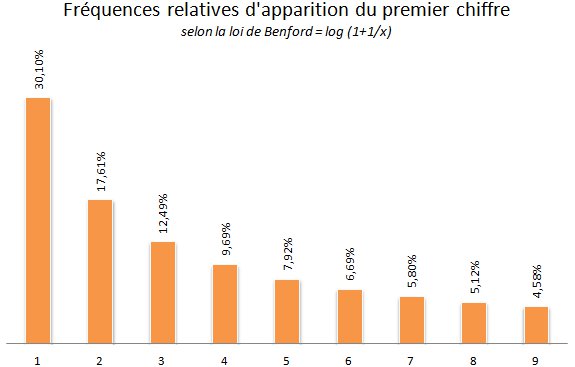
En tout cas, cette loi empirique a été démontrée mathématiquement et vérifiée expérimentalement sur d'immenses ensembles de données numériques. D'ailleurs, si la démonstration mathématique vous intéresse, je vous conseille la lecture de cette note intitulée : "Pourquoi la loi de Benford n'est pas mystérieuse".

Quelques conditions et domaines d'application

Pour assurer la significativité d'un jeu de données et rendre pertinente la comparaison avec cette loi logarithmique, il est nécessaire de disposer d'un grand nombre de données numériques, au moins plusieurs centaines. Pour que la loi soit applicable, il est également nécessaire que les nombres "s'étalent" sur plusieurs ordres de grandeurs (0.01 à 0.09, 0.1 à 0.9, 1 à 9, 10 à 99, 100 à 999 etc...). Il peut s'agir de données "naturelles" (superficie de lacs, longueur de fleuves, hauteur de sommets...) ou socio-économiques (statistiques sportives, démographiques, financières...).

Mais méfiance, car dans la vie courante, il n'est pas rare d'extraire des nombres ne vérifiant pas la loi : c'est notamment le cas des prix dans le commerce s'expliquant par le fait qu'on joue sur la perception des "seuils psychologiques" en affichant un prix de 1.99€ au lieu de 2€ par exemple. Par ailleurs, nous pouvons réaliser une expérience avec Google Books Ngram Viewer :

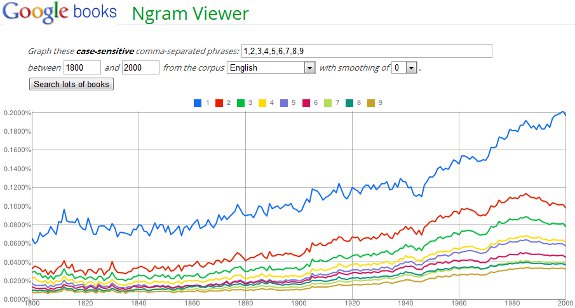
Bien que la série mesurée ne repose que sur un seul ordre de grandeur (mais prenant en compte une quantité colossale de données grâce au corpus d'ouvrages exploité par l'outil), on observe le respect de l'ordre d'apparition du premier chiffre (qui est en réalité un nombre dans ce cas) ainsi que des fréquences relativement proches de celles de référence.

Quid des données démographiques issues du recensement français ?

Le recensement de la population est particulièrement intéressant puisqu'il concilie à la fois une répartition sociodémographique (donc à priori indépendante et compatible avec l'application de la loi de Benford) et un risque d'anomalie engendré soit par l'erreur humaine (biais involontaire), soit par la fraude (biais volontaire). Car il existe en effet d'importants enjeux liés directement au nombre d'habitants de chaque commune, notamment des enjeux financiers (le versement de la DGF, le barème de certaines taxes, les indemnités versées aux maires et adjoints au maire) ou commerciaux (implémentation d'un certain nombre d'officines de pharmacie et débits de tabac). Au total, ce sont plusieurs centaines d'articles législatifs dont l'application est directement fonction de la population légale (par exemple, la commune de Saint Loup sur Semouse espérait compter plus de 3500 habitants et celle de Beuvry plus de 10000 habitants à l'issue du recensement 2009).

L'INSEE met à notre disposition un fichier Excel contenant l'exhaustivité des données de population, notamment pour chaque commune. Nous disposons ainsi des populations légales (en vigueur au 1er janvier 2012) pour les 36722 communes françaises. Comme nous l'explique l'INSEE, c'est la population dite "totale" qui est la plus souvent utilisée pour l'application de dispositions législatives ou réglementaires.

Voici donc les fréquences d'apparition des premiers chiffres relevés sur la population totale des communes (il a fallu ignorer 6 communes comptant zéro habitant) :

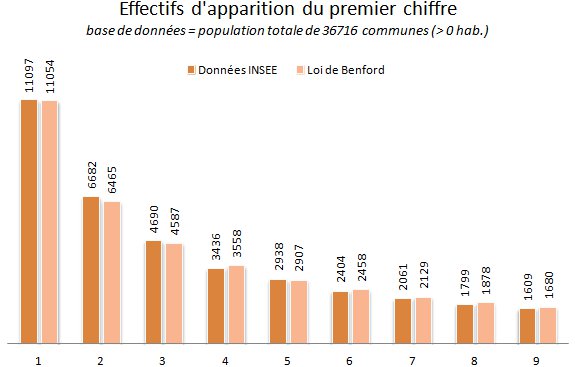
De prime abord, les écarts entre la loi de Benford et la répartition des données de l'INSEE sont très faibles puisqu'ils oscillent entre -4.2% (pour les chiffres 8 et 9) et +3.4% (pour le chiffre 2). Mais il est possible d'aller plus loin en confrontant les données de recensement et la loi de Benford sur les fréquences d'apparition des deux premiers chiffres. Voici les écarts obtenus en pourcentages (cette fois, il a fallu ignorer les 28 communes comptant moins de 10 habitants) :

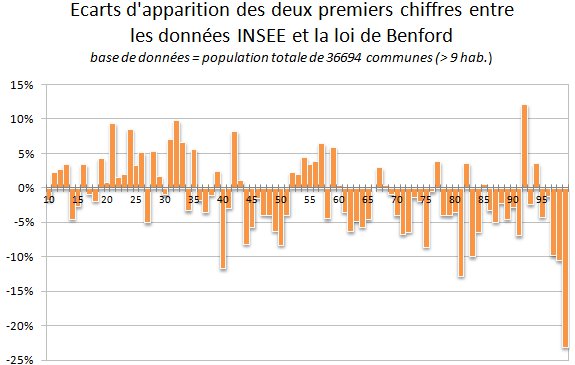
On commence à entrevoir des écarts en pourcentage plus importants, notamment sur "99" (-23%), "81" (-13%) ou "92" (+12%), mais en réalité, à l'échelle de la distribution toute entière, cela reste encore très largement marginal (l'écart sur "99" ne représente en fait que 37 communes). On pourrait éventuellement s'attendre à une nette sur-représentation sur "10" et "35" (correspondant aux paliers législatifs de 3500 et 10000 habitants), mais ce n'est pas le cas. En complément, bien qu'elle ait été mathématiquement démontrée, il convient de rappeler que la loi de Benford repose sur des observations empiriques : son application ne colle donc jamais parfaitement à la réalité.

Une autre considération : et le chiffre des unités ?

Psychologiquement, il serait bien sûr plus compliqué de frauder en imitant la loi de Benford, plutôt qu'en adaptant les chiffres des unités à la loi uniforme (chaque chiffre des unités possède en effet la même probabilité d'apparaître). Et d'ailleurs, compte tenu des intérêts décrits plus haut, on pourrait imaginer une fraude visant à gonfler un nombre à sa dizaine supérieure sans que cela ne soit trop voyant, et préférer pour cela un chiffre différent de zéro (car, à tort ou à raison, les comptes "ronds" sont souvent pressentis comme suspect).

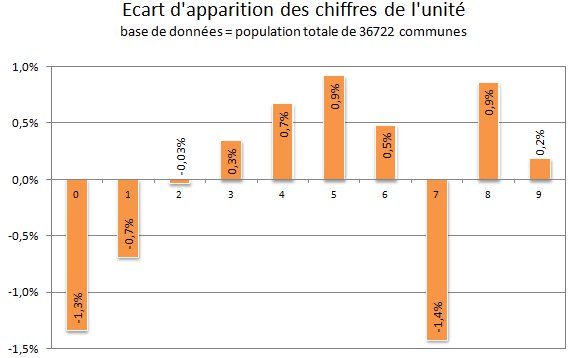
Les chiffres "0" (-1.3%) et "7" (-1.4%) sont apparemment les plus sous-représentés, tandis que les chiffres "5" et "8" (+0.9%) sont les plus sur-représentés. Compte tenu des écarts observés (en effectif, cela ne dépasse jamais plus d'une cinquantaine de communes), les résultats ne révèlent aucune anomalie significative.

Enfin, pour tout ceux qui souhaiteraient creuser ou vérifier les données de cet article, je mets à votre disposition le fichier Excel (clic droit puis enregistrer sous) contenant les formules, tableaux et graphiques ayant servi pour cet article.